Stress strain curve for mild steel with definition of stress and strain
The stress strain curve for mild steel typically exhibits several distinct regions that describe its mechanical behaviour under load. Mild steel is known for its relatively elastic and ductile properties, making it widely used in various structural and industrial applications. Here’s a general description of the stress-strain curve for mild steel:
Elastic Region (Proportional Limit):
In the initial stage of loading, as stress (force per unit area) is applied to the mild steel specimen, it deforms elastically. This means that the material returns to its original shape once the load is removed, and the stress-strain relationship is linear. This linear relationship is described by Hooke’s Law: stress is directly proportional to strain. The slope of this linear portion is known as the elastic modulus (Young’s modulus).
Yield Point and Yielding:
Beyond the proportional limit, mild steel transitions into the yield region. As the applied stress increases, the material starts to undergo permanent deformation or plastic deformation. The point at which this transition occurs is known as the yield point. Mild steel typically doesn’t exhibit a well-defined yield point, but instead, it shows a gradual yielding behavior. Yielding is characterized by a relatively flat or gently sloping portion on the stress-strain curve.
Plastic Deformation:
After yielding, the stress-strain curve continues to rise, indicating further plastic deformation. This means that the material continues to deform under load, but it no longer returns to its original shape when the load is removed. The material’s ability to absorb energy through plastic deformation makes it desirable for applications requiring toughness and ductility.
Ultimate Tensile Strength (UTS):
The stress-strain curve reaches its maximum point, known as the ultimate tensile strength (UTS), where the material experiences its highest stress before failure. The UTS represents the maximum load the material can withstand before it fractures.
Necking and Fracture:
Following the UTS, the stress-strain curve starts to decline as the material undergoes localized deformation, leading to necking. Necking is a phenomenon where the cross-sectional area of the material decreases significantly at a specific point, causing stress concentration. Eventually, the material reaches its breaking point, and fracture occurs.
Fracture Region:
The stress drops sharply after necking, indicating the onset of material fracture. This is the point at which the mild steel specimen breaks apart, and the stress decreases rapidly until the material can no longer support any load.
It’s important to note that the exact shape and behaviour of the stress-strain curve can vary based on factors such as the specific composition of the mild steel, the manufacturing process, and testing conditions. The general trends described above, however, are characteristic of mild steel’s mechanical response to loading.
Before understanding stress strain curve for mild steel, we need to familiar with some basic terms related to the topic.
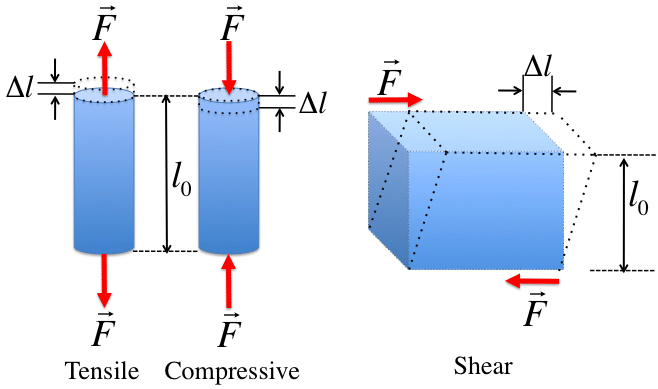
Stress definition
If applied force cause change in dimension, that materials is said to be under stress. This force per unit area is the measurement of stress. Higher the force per unit area, higher is stress.
There are three different nature of stress based on area of application. If the area is perpendicular to applied force, then stress can be tensile or compressive as per direction of force. For shear force, area parallel to force is considered for calculation of stress.
Thus force can be tensile, compressive and shear.
Tensile and compressive stress are known as direct stress.
Direct stress is denoted by Greek letter sigma (σ). while shear stress is denoted by Greek letter tau (τ).
SI unit of stress is N/m2 or Pascal (Pa). 1 N/m2 = 1 Pa
Imperial unit of stress is pound-force per square inch (psi)
(Please note that units of stress and pressure are equal)
σ (Stress) = Force / Area = F/A , where force in N and area in m2
If 1 N force is applied on area of 1 m2, then stress is 1 Pa.
Usually, for day to day calculation, stress unit considered is Mega Pascal (MPa)
Strain definition
Strain can be defined as change in dimension with respect to original dimension, when material is stressed.
Strain is denoted by Greek letter epsilon (ε).
ε (Strain) = Change in dimension / Original dimension
ε = ΔL / L , where L can be any dimension
Strain respective to shear force is termed as shear strain and denoted by Greek letter gamma. (γ)
Stress strain curve for mild steel
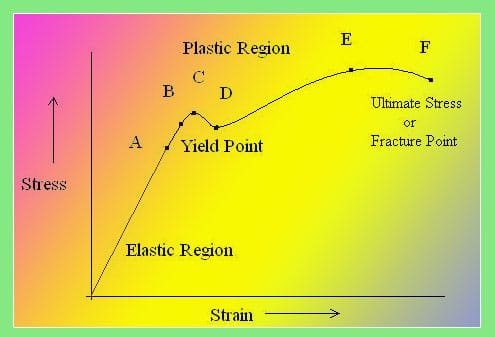
When a ductile material like mild steel is subjected to tensile force, it undergoes different stages before failure. Stress strain curve is the graphical representation of this stages. Different material may have different curve. Usually ductile materials follow similar pattern., so is for brittle materials. Here is the explanation of stress strain curve for mild steel which is ductile material.
Here is the list of different stages when ductile material subjected to force till its failure.
- Proportional limit (point A)
- Elastic limit (point B)
- Yield point ( upper yield point C and lower yield point D)
- Ultimate stress point (point E)
- Breaking point (point F)
Proportional limit
As shown in stress strain curve for mild steel, up to the point A, stress and strain follow a relationship. This is known as Hook’s law. Up to the limit of proportionality, stress directly followed the strain. This means ratio of stress and strain remains constant
Elastic limit
Up to this limit (point B), is material will regain its original shape is unloaded. Point B is known as elastic point.
Yield limit
When material is loaded beyond its elastic limit, it will not regain its original shape. There will be always some deformation.
Ultimate stress
This is the maximum stress a material can bear. Value of stress correspond to peak point on stress strain curve for mild steel is the ultimate stress. It is denoted by point E in diagram.
Breaking stress
Point on the stress strain curve where material fails, is known as breaking point. Stress correspond to this point is known as breaking stress.
Summary of stress strain curve for mild steel
Based on detailed explanation of stress strain curve for mild steel, we are able to identify different characteristic of mild steel under varying stress condition. Stress strain curve help up to identify two most important things. maximum stress a material can bear, stress at which material will fail. This help us to design machine cormorants for various application.
Also Read: Types of load in strength of material



excellent
Hello, I offer you my service, I am a master degrees student. I used from 1860 for pt tendon in the model I have simulated for my thesis. Now I need the strain – stress graph, please send it to me.
Hey very nice blog!